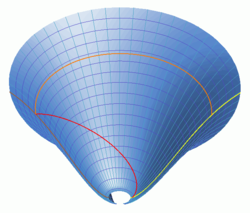

Spacetime is highly curved at cosmological scales, and as a result the expansion of the universe is inherently general relativistic; it cannot be understood with special relativity alone. The images to the right show two views of the large-scale geometry of the universe according to the ΛCDM cosmological model. Two of the dimensions of space are omitted, leaving one dimension of space and one of time. The narrow circular end of the diagram corresponds to a cosmological time of 700 million years after the big bang; the wide end is a cosmological time of 18 billion years, where one can see the beginning of the accelerating expansion which eventually dominates in this model. The purple grid lines mark off cosmological time at intervals of one billion years from the big bang. The cyan grid lines mark off comoving distance at intervals of one billion light years. Note that the circular curling of the surface is an artifact of the embedding with no physical significance; space does not actually curl around on itself. (A similar effect can be seen in the tubular shape of the pseudosphere.)
The brown line on the diagram is the worldline of the Earth (or, at earlier times, of the matter which condensed to form the Earth). The yellow line is the worldline of the most distant known quasar. The red line is the path of a light beam emitted by the quasar about 13 billion years ago and reaching the Earth in the present day. The orange line shows the present-day distance between the quasar and the Earth, about 28 billion light years.
According to the equivalence principle of general relativity, the rules of special relativity are locally valid in small regions of spacetime that are approximately flat. In particular, light always travels locally at the speed c; in our diagram, this means that light beams always make an angle of 45° with the local grid lines. It does not follow, however, that light travels a distance ct in a time t, as the red worldline illustrates. While it always moves locally at c, its time in transit (about 13 billion years) is not related to the distance traveled in any simple way. In fact the distance traveled is inherently ambiguous because of the changing scale of the universe. Nevertheless, we can single out two distances which appear to be physically meaningful: the distance between the Earth and the quasar when the light was emitted, and the distance between them in the present era. The former distance is about 4 billion light years, much smaller than ct. The latter distance (shown by the orange line) is about 28 billion light years, much larger than ct. Note that the light took much longer than 4 billion years to reach us though it was emitted from only 4 billion light years away. In fact, we can see from the diagram that the light was moving away from the Earth when it was first emitted, in the sense that the metric distance to the Earth increased with cosmological time for the first few billion years of its travel time. None of this surprising behavior originates from a special property of metric expansion, but simply from local principles of special relativity integrated over a curved surface.
What is the universe expanding into?
The universe is not expanding into anything, almost by definition; there is simply more space at later times than at earlier times. It may be that the size of the universe is infinite, which is easy to conceptualize.
Even if the universe is finite, it is possible to make more space without having any "outside" space. A common analogy is to consider that it is possible to increase the surface area of a balloon by inflating it, without needing any additional balloons to facilitate the expansion. However, a balloon is a two-dimensional surface expanding into a three-dimensional space. There is not theorized to be a higher-dimensional space into which three-dimensional space is expanding; more of it simply appears as if by stretching.[7] However, since space and time are coequal dimensions, some theorists believe that three-dimensional space is expanding into the temporal dimension. For example, using the previous balloon analogy, the surface area increases as the radius of the balloon increases. The radius is essentially the temporal dimension, i.e. the universe is expanding into time.
This finite universe theory supposes that the universe has no "edge", but wraps around on itself. If it were possible to travel the entire length of the universe without going faster than light, one would simply end up back in the same place (but not in the same time), not unlike going all the way around the surface of the balloon (or a planet like the Earth).
The notion of "more space" is local, not global; we do not know how much space there is in total. The embedding diagram has been arbitrarily cut off a few billion years past the Earth and the quasar, but it could be extended indefinitely, even infinitely, provided we imagine it as curling into a "spiral of constant radius" rather than a circle. Even if the overall spatial extent is infinite we still say that space is expanding because, locally, the characteristic distance between objects is increasing.
Local perturbations
The expansion of space is sometimes described as a force which acts to push objects apart. Though this is an accurate description of the effect of the cosmological constant, it is not an accurate picture of the phenomenon of expansion in general. For much of the universe's history the expansion has been due mainly to inertia. The matter in the very early universe was flying apart for unknown reasons (most likely as a result of cosmic inflation) and has simply continued to do so, though at an ever-decreasing rate due to the attractive effect of gravity. In addition to slowing the overall expansion, gravity causes local clumping of matter into stars and galaxies. These stars and galaxies do not subsequently expand, there being no force compelling them to do so. There is no essential difference between the inertial expansion of the universe and the inertial separation of nearby objects in a vacuum; the former is simply a large-scale extrapolation of the latter. A uniform local "explosion" of matter can be locally described by the FLRW geometry, the same geometry which describes the expansion of the universe as a whole. In particular, general relativity predicts that light will move at the speed c with respect to the local motion of the exploding matter, a phenomenon analogous to frame dragging.
This situation changes somewhat with the introduction of a cosmological constant. A cosmological constant has the effect of a repulsive force between objects which is proportional (not inversely proportional) to distance. Unlike inertia it actively "pulls" on objects which have clumped together under the influence of gravity, and even on individual atoms. However this does not cause the objects to grow steadily or to disintegrate; unless they are very weakly bound, they will simply settle into an equilibrium state which is slightly (undetectably) larger than it would otherwise have been. As the universe expands and the matter in it thins, the gravitational attraction decreases (since it is proportional to the density), while the cosmological repulsion increases; thus the ultimate fate of the ΛCDM universe is a near vacuum expanding at an ever increasing rate under the influence of the cosmological constant. However the only locally visible effect of the accelerating expansion is the disappearance (by runaway redshift) of distant galaxies; gravitationally bound objects like the Milky Way do not expand.
Other models of expansion
The expansion of space is often illustrated with models which show only the size of space at a particular time, leaving the dimension of time implicit.
In the "ant on a rubber rope model" one imagines an ant (idealized as pointlike) crawling at a constant speed on a perfectly elastic rope which is constantly stretching. If we stretch the rope in accordance with the ΛCDM scale factor and think of the ant's speed as the speed of light, then this analogy is numerically accurate—the ant's position over time will match the path of the red line on the embedding diagram above.
In the "rubber sheet model" one replaces the rope with a flat two-dimensional rubber sheet which expands uniformly in all directions. The addition of a second spatial dimension raises the possibility of showing local perturbations of the spatial geometry by local curvature in the sheet.
In the "balloon model" the flat sheet is replaced by a spherical balloon which is inflated from an initial size of zero (representing the big bang). A balloon has positive Gaussian curvature while observations suggest that the real universe is spatially flat, but this inconsistency can be eliminated by making the balloon very large so that it is locally flat to within the limits of observation. This analogy is potentially confusing since it wrongly suggests that the big bang took place at the center of the balloon. In fact points off the surface of the balloon have no meaning, even if they were occupied by the balloon at an earlier time.
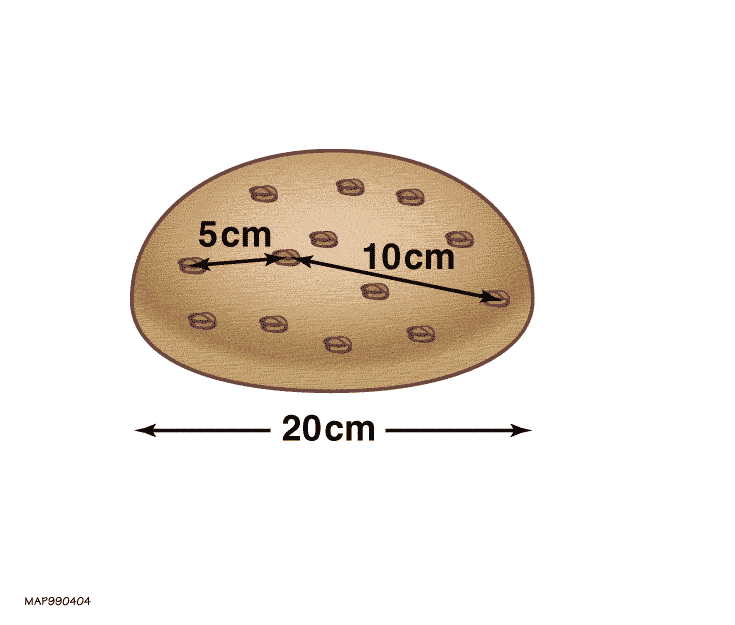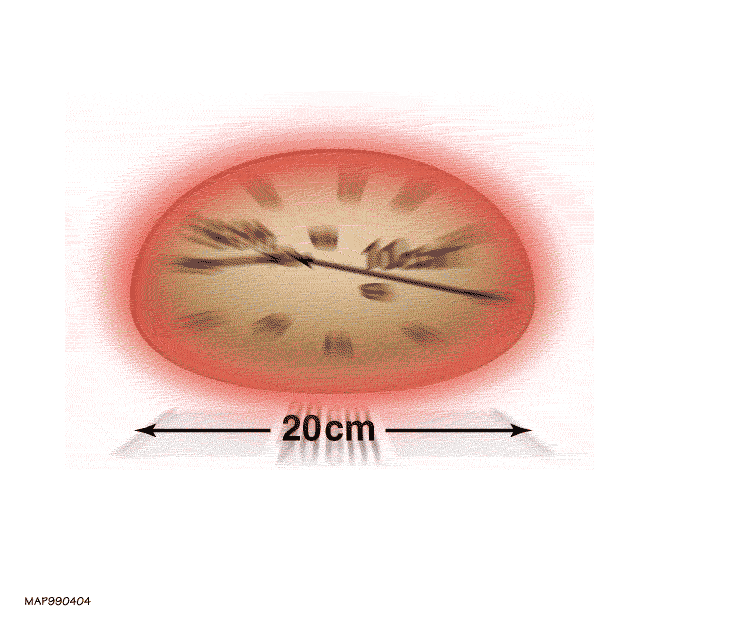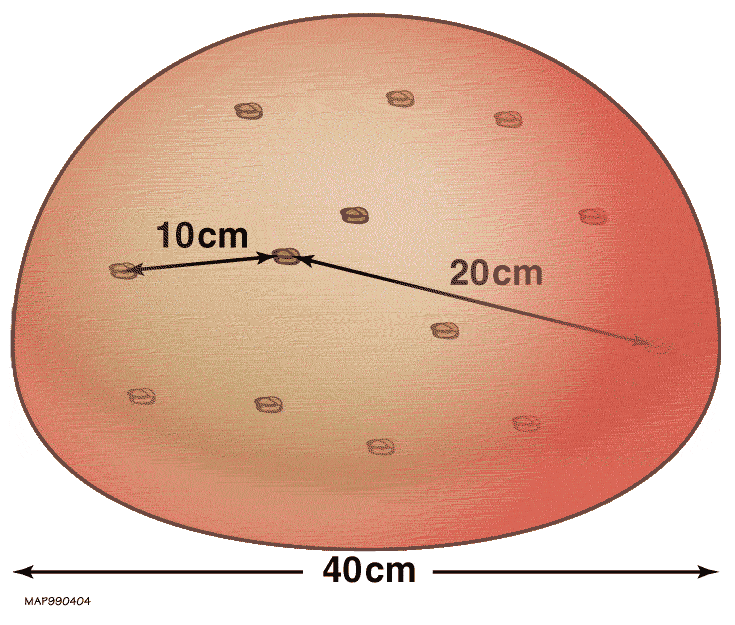
In the "raisin bread model" one imagines a loaf of raisin bread expanding in the oven. The loaf (space) expands as a whole, but the raisins (gravitationally bound objects) do not expand; they merely grow farther away from each other.
All of these models have the conceptual problem of requiring an outside force acting on the "space" at all times to make it expand. Unlike real cosmological matter, sheets of rubber and loaves of bread are bound together electromagnetically and will not continue to expand on their own after an initial tug.
Main article: Metric (mathematics)
Metric expansion is not something that most humans are aware of, on a day to day basis. To understand the expansion of the universe, it is helpful to discuss briefly, what a metric is, and how metric expansion works.
Definition of a metric
A metric defines how a distance can be measured between two nearby points in space, in terms of the coordinates of those points. A coordinate system locates points in a space (of whatever number of dimensions) by assigning unique numbers known as coordinates, to each point. The metric is then a formula which converts coordinates of two points into distances.
Metric for Earth's surface
For example, consider the measurement of distance between two places on the surface of the Earth. This is a simple, familiar example of a non-Euclidean geometry. Because the surface of the Earth is two-dimensional, points on the surface of the earth can be specified by two coordinates—for example, the latitude and longitude. Specification of a metric requires that one first specify the coordinates used. In our simple example of the surface of the Earth, we could choose any kind of coordinate system we wish, for example latitude and longitude, or X-Y-Z Cartesian coordinates. Once we have chosen a specific coordinate system, the numerical values of the co-ordinates of any two points are uniquely determined, and based upon the properties of the space being discussed, the appropriate metric is mathematically established too. On the curved surface of the Earth, we can see this effect in long-haul airline flights where the distance between two points is measured based upon a Great circle, and not along the straight line that passes through the Earth. While there is always an effect due to this curvature, at short distances the effect is so small as to be unnoticeable.
[edit] Metric for spacetime
Points on the surface of the Earth can be specified by giving two coordinates. Because space-time is four dimensional, we must specify points in space-time by giving four coordinates. The most convenient coordinates to use for cosmology are called comoving coordinates. Because space appears to be Euclidean, on a large scale, one can specify the spatial coordinates in terms of x,y, and z coordinates, though other choices such as spherical coordinates are also commonly used. The fourth required coordinate is time, which is specified in comoving coordinates as cosmological time. Though large-scale space appears to be Euclidean, the same cannot be said for the metric of space-time. The non-Euclidean nature of space-time manifests itself by the fact that the distance between points with constant coordinates grows with time, rather than remaining constant.
Theoretical basis and first evidence
Hubble's law
Technically, the metric expansion of space is a feature of many solutions to the Einstein field equations of general relativity, and distance is measured using the Lorentz interval. This theoretical explanation provides a possible explanation of the observed Hubble's law which might indicate that galaxies that are more distant from us appear to be receding faster than galaxies that are closer to us.
In spaces that expand, the metric changes with time in a way that causes distances to appear larger at later times, so if our universe is a Big Bang universe, we would observe phenomena associated with metric expansion of space. If we lived in a space that contracted (a Big Crunch universe) we would observe phenomena associated with a metric contraction of space instead.
Cosmological constant and the Friedman equations
The first general relativistic models predicted that a universe which was dynamical and contained ordinary gravitational matter would contract rather than expand. Einstein's first proposal for a solution to this problem involved adding a cosmological constant into his theories to balance out the contraction, in order to obtain a static universe solution. But in 1922 Alexander Friedman derived a set of equations known as the Friedmann equations, showing that the universe might expand and presenting the expansion speed in this case.[8] The observations of Edwin Hubble in 1929 suggested that distant galaxies were all apparently moving away from us, so that many scientists came to accept that the universe was expanding.
Hubble's personal opinion upon interpretation of the data
These scientists however did not include Hubble himself. While the metric expansion of space reading of Hubble's 1929 observations is viewed today by most scientists as the correct reading of the data, Hubble wrote six years later:
"… if redshift are not primarily due to velocity shift … the velocity-distance relation is linear, the distribution of the nebula is uniform, there is no evidence of expansion, no trace of curvature, no restriction of the time scale … and we find ourselves in the presence of one of the principle of nature that is still unknown to us today … whereas, if redshifts are velocity shifts which measure the rate of expansion, the expanding models are definitely inconsistent with the observations that have been made … expanding models are a forced interpretation of the observational results"
– E. Hubble, Ap. J., 84, 517, 1936 [9]
"[If the redshifts are a Doppler shift] … the observations as they stand lead to the anomaly of a closed universe, curiously small and dense, and, it may be added, suspiciously young. On the other hand, if redshifts are not Doppler effects, these anomalies disappear and the region observed appears as a small, homogeneous, but insignificant portion of a universe extended indefinitely both in space and time."
– E. Hubble, Monthly Notices of the Royal Astronomical Society, 97, 506, 1937 [10]
Inflation an explanation for the expansion
While Hubble's words were forgotten, the notion of the expansion of the universe became consensus. Until the theoretical developments in the 1980s no one had an explanation for why this seemed to be the case, but with the development of models of cosmic inflation, the expansion of the universe became a general feature resulting from vacuum decay. Accordingly, the question "why is the universe expanding?" is now answered by understanding the details of the inflation decay process which occurred in the first 10−32 seconds of the existence of our universe. It is suggested that in this time the metric itself changed exponentially, causing space to change from smaller than an atom to around 100 million light years across.

Measuring distance in a metric space
In expanding space, distance is a dynamical quantity which changes with time. There are several different ways of defining distance in cosmology, known as distance measures, but the most common is comoving distance.
The metric only defines the distance between nearby points. In order to define the distance between arbitrarily distant points, one must specify both the points and a specific curve connecting them. The distance between the points can then be found by finding the length of this connecting curve. Comoving distance defines this connecting curve to be a curve of constant cosmological time. Operationally, comoving distances cannot be directly measured by a single Earth-bound observer. To determine the distance of distant objects, astronomers generally measure luminosity of standard candles, or the redshift factor 'z' of distant galaxies, and then convert these measurements into distances based on some particular model of space-time, such as the Lambda-CDM model.
Observational evidence
Theoretical cosmologists developing models of the universe have drawn upon a small number of reasonable assumptions in their work. These workings have led to models in which the metric expansion of space is a likely feature of the universe. Chief among the underlying principles that result in models including metric expansion as a feature are:
- the Cosmological Principle which demands that the universe looks the same way in all directions (isotropic) and has roughly the same smooth mixture of material (homogeneous).
- the Copernican Principle which demands that no place in the universe is preferred (that is, the universe has no "starting point").
Scientists have tested carefully whether these assumptions are valid and borne out by observation. Observational cosmologists have discovered evidence - very strong in some cases - that supports these assumptions, and as a result, metric expansion of space is considered by cosmologists to be an observed feature on the basis that although we cannot see it directly, scientists have tested the properties of the universe and observation provides compelling confirmation. Sources of this confidence and confirmation include:
- Hubble demonstrated that all galaxies and distant astronomical objects were moving away from us, as predicted by a universal expansion.[11] Using the redshift of their electromagnetic spectra to determine the distance and speed of remote objects in space, he showed that all objects are moving away from us, and that their speed is proportional to their distance, a feature of metric expansion. Further studies have since shown the expansion to be extremely isotropic and homogeneous, that is, it does not seem to have a special point as a "center", but appears universal and independent of any fixed central point.
- In studies of large-scale structure of the cosmos taken from redshift surveys a so-called "End of Greatness" was discovered at the largest scales of the universe. Until these scales were surveyed, the universe appeared "lumpy" with clumps of galaxy clusters and superclusters and filaments which were anything but isotropic and homogeneous. This lumpiness disappears into a smooth distribution of galaxies at the largest scales in much the same way a Jackson Pollock painting looks lumpy close-up, but more regular as a whole.
- The isotropic distribution across the sky of distant gamma-ray bursts and supernovae is another confirmation of the Cosmological Principle.
- The Copernican Principle was not truly tested on a cosmological scale until measurements of the effects of the cosmic microwave background radiation on the dynamics of distant astrophysical systems were made. A group of astronomers at the European Southern Observatory noticed, by measuring the temperature of a distant intergalactic cloud in thermal equilibrium with the cosmic microwave background, that the radiation from the Big Bang was demonstrably warmer at earlier times.[12] Uniform cooling of the cosmic microwave background over billions of years is explainable only if the universe is experiencing a metric expansion.
Taken together, the only theory which coherently explains these phenomena relies on space expanding through a change in metric. Interestingly, it was not until the discovery in the year 2000 of direct observational evidence for the changing temperature of the cosmic microwave background that more bizarre constructions could be ruled out. Until that time, it was based purely on an assumption that the universe did not behave as one with the Milky Way sitting at the middle of a fixed-metric with a universal explosion of galaxies in all directions (as seen in, for example, an early model proposed by Milne). Yet before this evidence, many rejected the Milne viewpoint based on the Mediocrity principle.
Additionally, scientists are confident that the theories which rely on the metric expansion of space are correct because they have passed the rigorous standards of the scientific method. In particular, when physics calculations are performed based upon the current theories (including metric expansion), they appear to give results and predictions which, in general, agree extremely closely with both astrophysical and particle physics observations. The spatial and temporal universality of physical laws was until very recently taken as a fundamental philosophical assumption that is now tested to the observational limits of time and space. This evidence is taken very seriously because the level of detail and the sheer quantity of measurements which the theories predict can be shown to precisely and accurately match visible reality. The level of precision is difficult to quantify, but is on the order of the precision seen in the physical constants that govern the physics of the universe.

No comments:
Post a Comment